Cours chapitre 5 Fonctions (Aspect graphique)

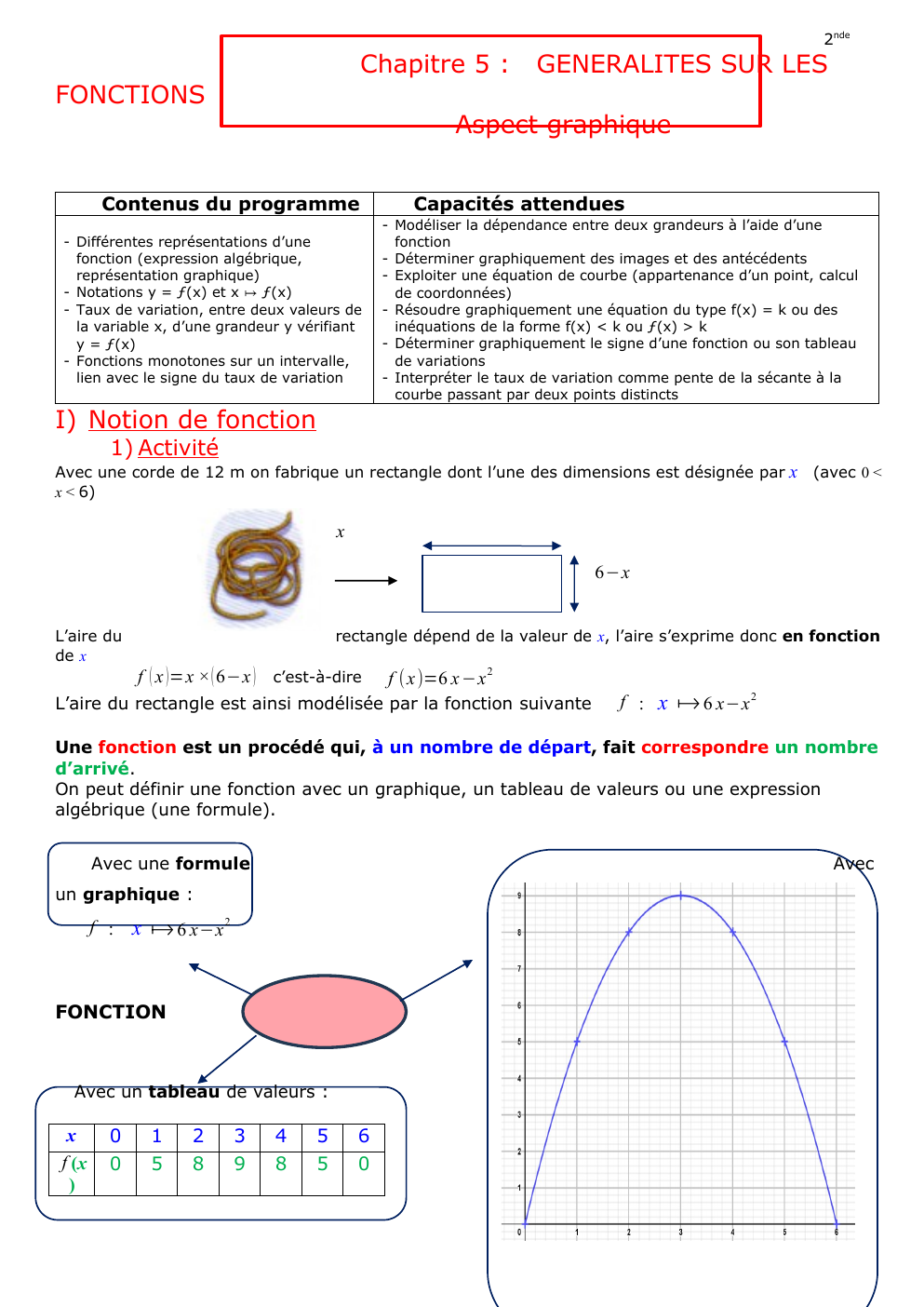
« Chapitre 5 : FONCTIONS 2nde GENERALITES SUR LES Aspect graphique Contenus du programme - Différentes représentations d’une fonction (expression algébrique, représentation graphique) - Notations y = ƒ(x) et x ↦ ƒ(x) - Taux de variation, entre deux valeurs de la variable x, d’une grandeur y vérifiant y = ƒ(x) - Fonctions monotones sur un intervalle, lien avec le signe du taux de variation Capacités attendues - Modéliser la dépendance entre deux grandeurs à l’aide d’une fonction - Déterminer graphiquement des images et des antécédents - Exploiter une équation de courbe (appartenance d’un point, calcul de coordonnées) - Résoudre graphiquement une équation du type f(x) = k ou des inéquations de la forme f(x) < k ou ƒ(x) > k - Déterminer graphiquement le signe d’une fonction ou son tableau de variations - Interpréter le taux de variation comme pente de la sécante à la courbe passant par deux points distincts I) Notion de fonction 1) Activité Avec une corde de 12 m on fabrique un rectangle dont l’une des dimensions est désignée par x (avec 0 < x < 6) x 6−x L’aire du de x rectangle dépend de la valeur de x, l’aire s’exprime donc en fonction f ( x )=x × ( 6−x ) c’est-à-dire f (x )=6 x −x 2 L’aire du rectangle est ainsi modélisée par la fonction suivante f : x ⟼ 6 x−x 2 Une fonction est un procédé qui, à un nombre de départ, fait correspondre un nombre d’arrivé. On peut définir une fonction avec un graphique, un tableau de valeurs ou une expression algébrique (une formule). Avec une formule Avec un graphique : f : x ⟼ 6 x−x 2 FONCTION Avec un tableau de valeurs : x f (x ) 0 0 1 5 2 8 3 9 4 8 5 5 6 0 2) Définition, notation et vocabulaire Soit D un intervalle de R ou une réunion d’intervalles de R . On définit une fonction f sur D lorsqu’on fait correspondre à chaque nombre réel x de D un unique réel noté f (x). f (x) est appelé l’image de x f :D⟶ R x ⟼ f (x) On note D est appelé l’ensemble.... »