Correction - CS n°8 1ère Spécialité Maths

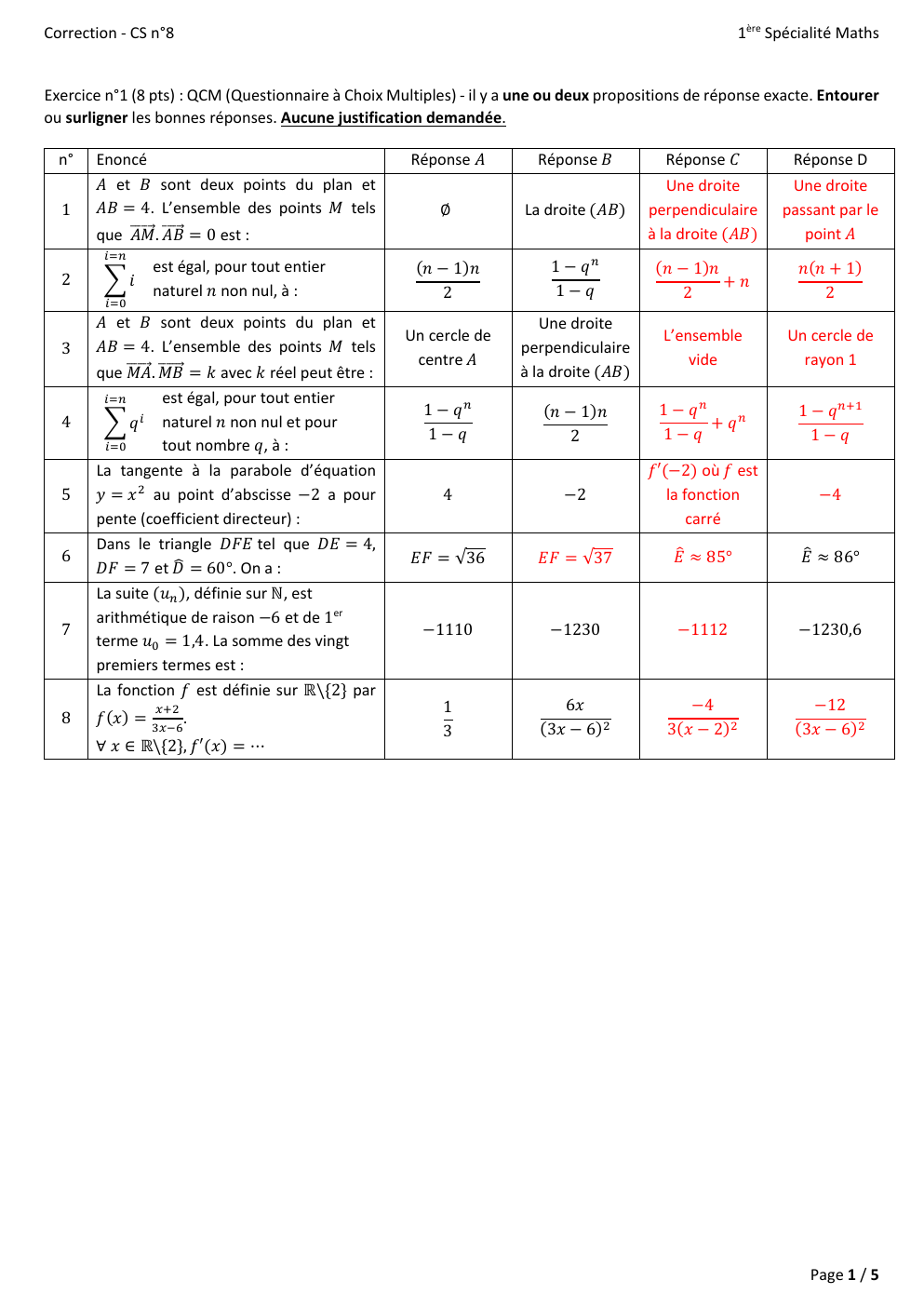
« Correction - CS n°8 1ère Spécialité Maths Exercice n°1 (8 pts) : QCM (Questionnaire à Choix Multiples) - il y a une ou deux propositions de réponse exacte.

Entourer ou surligner les bonnes réponses.

Aucune justification demandée. n° 1 2 3 4 5 6 7 8 Enoncé 𝐴𝐴 et 𝐵𝐵 sont deux points du plan et 𝐴𝐴𝐴𝐴 = 4.

L’ensemble des points 𝑀𝑀 tels �����⃗ = 0 est : que ������⃗ 𝐴𝐴𝐴𝐴.

𝐴𝐴𝐴𝐴 𝑖𝑖=𝑛𝑛 est égal, pour tout entier naturel 𝑛𝑛 non nul, à : � 𝑖𝑖 𝑖𝑖=0 𝐴𝐴 et 𝐵𝐵 sont deux points du plan et 𝐴𝐴𝐴𝐴 = 4.

L’ensemble des points 𝑀𝑀 tels que ������⃗ 𝑀𝑀𝑀𝑀.

������⃗ 𝑀𝑀𝑀𝑀 = 𝑘𝑘 avec 𝑘𝑘 réel peut être : est égal, pour tout entier � 𝑞𝑞 naturel 𝑛𝑛 non nul et pour 𝑖𝑖=0 tout nombre 𝑞𝑞, à : La tangente à la parabole d’équation 𝑦𝑦 = 𝑥𝑥 2 au point d’abscisse −2 a pour pente (coefficient directeur) : Dans le triangle 𝐷𝐷𝐷𝐷𝐷𝐷 tel que 𝐷𝐷𝐷𝐷 = 4, � = 60°.

On a : 𝐷𝐷𝐷𝐷 = 7 et 𝐷𝐷 La suite (𝑢𝑢𝑛𝑛 ), définie sur ℕ, est arithmétique de raison −6 et de 1er terme 𝑢𝑢0 = 1,4.

La somme des vingt premiers termes est : La fonction 𝑓𝑓 est définie sur ℝ\{2} par 𝑖𝑖=𝑛𝑛 𝑖𝑖 𝑓𝑓(𝑥𝑥 ) = 𝑥𝑥+2 3𝑥𝑥−6 . ∀ 𝑥𝑥 ∈ ℝ\{2}, 𝑓𝑓′(𝑥𝑥) = ⋯ Réponse 𝐴𝐴 Réponse 𝐵𝐵 ∅ La droite (𝐴𝐴𝐴𝐴) Un cercle de centre 𝐴𝐴 Une droite perpendiculaire à la droite (𝐴𝐴𝐴𝐴) (𝑛𝑛 − 1)𝑛𝑛 2 1 − 𝑞𝑞 𝑛𝑛 1 − 𝑞𝑞 1 − 𝑞𝑞 𝑛𝑛 1 − 𝑞𝑞 (𝑛𝑛 − 1)𝑛𝑛 2 Réponse 𝐶𝐶 Réponse D Une droite perpendiculaire à la droite (𝐴𝐴𝐴𝐴) Une droite passant par le point 𝐴𝐴 L’ensemble vide Un cercle de rayon 1 1 − 𝑞𝑞 𝑛𝑛 + 𝑞𝑞 𝑛𝑛 1 − 𝑞𝑞 1 − 𝑞𝑞 𝑛𝑛+1 1 − 𝑞𝑞 (𝑛𝑛 − 1)𝑛𝑛 + 𝑛𝑛 2 𝑓𝑓′(−2) où 𝑓𝑓 est la fonction carré 𝑛𝑛(𝑛𝑛 + 1) 2 4 −2 −4 𝐸𝐸𝐸𝐸 = √36 𝐸𝐸𝐸𝐸 = √37 𝐸𝐸� ≈ 85° 𝐸𝐸� ≈ 86° −1110 −1230 −1112 −1230,6 1 3 6𝑥𝑥 (3𝑥𝑥 − 6)2 −4 3(𝑥𝑥 − 2)2 −12 (3𝑥𝑥 − 6)2 Page 1 / 5 Correction - CS n°8 1ère Spécialité Maths Question n°1 : Réponses 𝐶𝐶 et 𝐷𝐷. �����⃗ passant par 𝐶𝐶 tel que L’ensemble des points 𝑀𝑀 tels que ������⃗ 𝐴𝐴𝐴𝐴.

�����⃗ 𝐴𝐴𝐴𝐴 = 0 est une droite (𝑑𝑑𝑘𝑘 ) de vecteur normal 𝐴𝐴𝐴𝐴 𝑘𝑘 0 �����⃗ �����⃗ �����⃗ = 0.

Ainsi, les points 𝐴𝐴 et 𝐶𝐶 sont confondus.

La droite est perpendiculaire à la droite (𝐴𝐴𝐴𝐴) 𝐴𝐴𝐴𝐴 𝐴𝐴𝐴𝐴 = 2 𝐴𝐴𝐴𝐴 = �����⃗� �𝐴𝐴𝐴𝐴 et passe par 𝐴𝐴. 𝐴𝐴𝐴𝐴 Question n°2 : Réponses 𝐶𝐶 et 𝐷𝐷. 𝑖𝑖=𝑛𝑛−1 On sait que.... »